The proportion of vibrational energy transmitted by a vibration Isolator is given by:

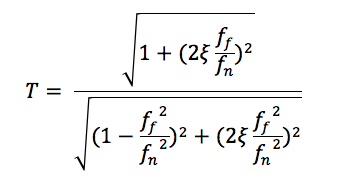
Where:

f_f = forcing frequency of vibration (Hz)
f_n = natural frequency of vibration isolator (Hz)

ξ = = critical damping ratio (typical values for steel 0.005 – 0.01; rubber 0.05 – 0.1)

m = mass (kg)
c = viscous damping (Nsm^-1)
ω_n = 2 π f_n

For lightly damped materials, such as steel springs, the critical damping ratio is negligible. The formula can then be simplified to:

This shows that when resonance occurs (f_f= f_n) T tends to infinity (i.e. there is significant amplification of the transmitted force rather than any isolation).

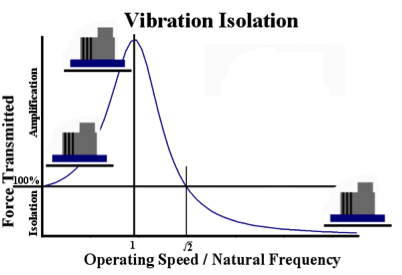
For isolation to occur T must be less than one, which only occurs when:

However, the actual performance of a vibration isolator can be compromised by several factors that must also be taken into account when designing or selecting a vibration Isolator [Find Out More].